Given: \( \dot{m}=200\,\text{kg/s} \),
\( A_{1}=0.7\,\text{m}^{2} \), \( p_{1}=1600\,\text{kPa} \), \( V_{1}=150\,\text{m/s} \),
\( A_{e}=2.4\,\text{m}^{2} \), \( p_{e}=80\,\text{kPa} \), \( V_{e}=2300\,\text{m/s} \).

To calculate: Thrust = ?.

The schematic diagram of the problem description is shown in Fig. 1.

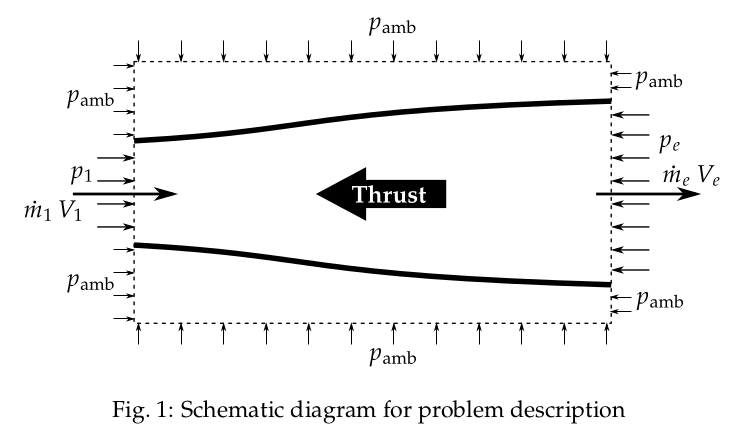
Considering the control volume around the nozzle, and applying conservation of momentum in the horizontal direction, the thrust force acting on the nozzle can be written as,

$$ \begin{aligned} \text{Thrust force on nozzle} =&\ \text{Rate of momentum leaving the nozzle} \\ & - \text{Rate on momentum entering the nozzle} \\ & + \text{pressure force on the exit plane} \\ & + \text{pressure force on the inlet plane} \end{aligned} $$ $$ \begin{aligned} \text{Thrust force on nozzle} =&\ \dot{m}_{e}V_{e} - \dot{m}_{1}V_{1} \\ & + p_{e}A_{e} + p_{\text{amb}}\left(A-A_{e}\right) \\ & - p_{1}A_{1}-p_{\text{amb}}\left(A-A_{1}\right) \end{aligned} $$

where \( A \) is an arbitrary area of the vertical side of the control volume. Simplifying this equation gives,

$$ \begin{aligned} \text{Thrust force on nozzle} =&\ \dot{m}_{e}V_{e}-\dot{m}_{1}V_{1} \\ & + p_{e}A_{e}-p_{1}A_{1} \\ & - p_{\text{amb}}\left(A_{e}-A_{1}\right)\ . \end{aligned} $$

Since \( \dot{m}_{1} = \dot{m}_{e} = \dot{m} \),

$$ \begin{aligned} \text{Thrust force on nozzle} =&\ \dot{m}\left(V_{e}-V_{1}\right) \\ & + p_{e}A_{e}-p_{1}A_{1} \\ & - p_{\text{amb}}\left(A_{e}-A_{1}\right)\ . \end{aligned} $$

Case 1. Assuming that the inlet pressure is same as the ambient pressure, \( p_{1}=p_{\text{amb}} \), the equation becomes,

$$ \text{Thrust force on nozzle}=\dot{m}\left(V_{e}-V_{1}\right)+\left(p_{e}-p_{1}\right)A_{e}\ . $$ $$ \text{Thrust force on nozzle} = 200\times\left(2300-150\right)+\left(80\times10^{3}-1600\times10^{3}\right)\times2.4\ . $$ $$ \boxed{\text{Thrust force on nozzle}=-3218\,\text{kN}}\ $$

Case 2) Assuming that the exit pressure is same as the ambient pressure, \( p_{e}=p_{\text{amb}} \), the equation becomes,

$$ \text{Thrust force on nozzle}=\dot{m}\left(V_{e}-V_{1}\right)+\left(p_{e}-p_{1}\right)A_{1}\ . $$ $$ \text{Thrust force on nozzle}=200\times\left(2300-150\right)+\left(80\times10^{3}-1600\times10^{3}\right)\times0.7\ . $$ $$ \boxed{\text{Thrust force on nozzle}=-634\,\text{kN}}\ . $$