Given: \( \gamma=1.3 \)
\( A_{1} = A_{e}=A \), \( V_{1} = 120\,\text{m/s} \), \( T_{1} = 200^{\circ}\,\text{C} = 473\,\text{K} \), \( p_{1} = 700\,\text{kPa} \),
\( V_{e} = 240\,\text{m/s} \), \( T_{e} = 450^{\circ}\,\text{C} = 723\,\text{K} \).

To calculate: \( \dot{q}/\dot{m}=? \), \( \dot{m}/A=? \).

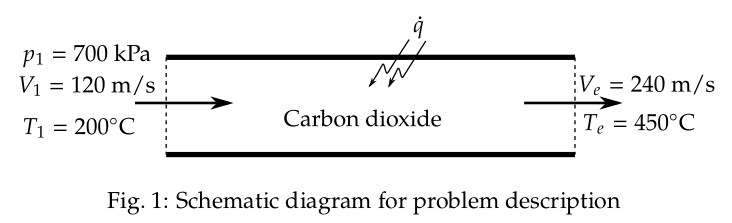
The schematic diagram of the problem description is shown in Fig. 1.

Using the molar mass of cardon-dioxide \( \left(\text{CO}_{2}\right) \) as \( 12\times1_{\text{C}}+16\times2_{\text{O}}=44\,\text{kg/kmol} \) and the universal gas constant as \( 8314\,\text{J/kmol-K} \), the gas constant can be written as,

$$ R=\frac{R_{u}}{\hat{m}}=\frac{8314}{44}=188.95\,\text{J/kg-K}\ . $$

The heat capacity at constant pressure can be calculated as,

$$ c_{p}=\frac{\gamma\,R}{\gamma-1}=\frac{1.3\times188.95}{1.3-1}=818.78\,\text{J/kg-K}\ . $$

Applying the conservation of energy principle,

$$ c_{p}T_{1}+\frac{V_{1}^{2}}{2}+\dot{q}/\dot{m}=c_{p}T_{e}+\frac{V_{e}^{2}}{2} $$ $$ 818.78\times473+\frac{120^{2}}{2}+\dot{q}/\dot{m}=818.78\times723+\frac{240^{2}}{2} $$

We can solve for the heat added per unit mass to be,

$$ \dot{q}/\dot{m}=818.78\times723+\frac{240^{2}}{2}-818.78\times473-\frac{120^{2}}{2} $$ $$ \boxed{\dot{q}/\dot{m}=226295\,\text{J/kg}}\ . $$

The density at the inlet can be calculated using the ideal gas equation to be,

$$ \rho_{1}=\frac{p_{1}}{R\,T_{1}}=\frac{700\times10^{3}}{188.95\times473}=7.8323\,\text{kg/m}^{3} $$

The mass flow rate,

$$ \dot{m}=\rho_{1}A_{1}V_{1} $$

which gives the mass flow rate per unit area as,

$$ \dot{m}/A=\rho_{1}V_{1}=7.8323\times120 $$ $$ \boxed{\dot{m}/A=939.876\,\text{kg/s-m}^{2}}\ . $$