Problem 1.13

In a proposed jet propulsion system for an automobile, air is drawn in vertically through a large intake in the roof at a rate of kg/s, the velocity through this intake being small. Ambient pressure and temperature are kPa and ^oC, respectively. This air is compressed and heated and then discharged horizontally out of a nozzle at the rear of the automobile at a velocity of m/s and a pressure of kPa. If the rate of heat addition to the air stream is kW, find the nozzle discharge area and the thrust developed by the system.

Given:
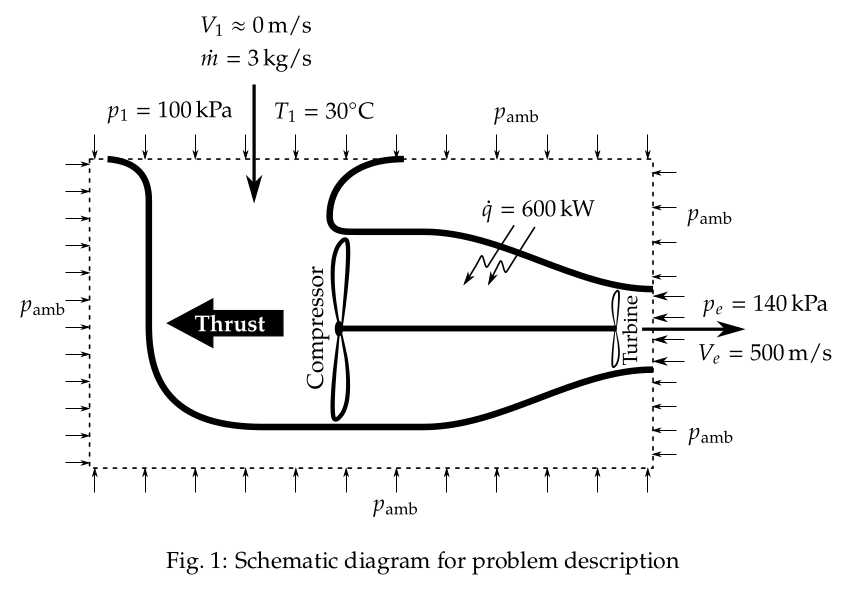
Air is drawn vertically, $ \dot{m}=3\,\text{kg/s} $, $ V_{1}\approx0\,\text{m/s} $, $ p_{\text{amb}}=p_{0}=100\,\text{kPa} $, $ T_{\text{amb}}=T_{0}=30^{\circ}\,\text{C}=303\,\text{K} $.
Air is compressed and heated and discharged horizontally, $ V_{e}=500\,\text{m/s} $, $ p_{e}=140\,\text{kPa} $, $ \dot{q}=600\,\text{kW} $.

To calculate: $ A_{e}=? $, $ \text{Thrust}=? $.

The schematic diagram of the problem description is shown in Fig. 1.

Applying the conservation of energy through the system,

$$ \begin{aligned} \text{Rate of energy entering}\ &+\ \text{Rate of heat addition} \\ &=\text{Rate of energy leaving}\ +\ \text{Work done by the system} \end{aligned} $$ $$ \dot{m}\,c_{p}T_{0}+\dot{q}=\dot{m}\,c_{p}T_{e}+\dot{m}\,\frac{V_{e}^{2}}{2}+W $$

$$ 3\times1005\times303+600\times10^{3}=3\times1005\times T_{e}+3\times\frac{500^{2}}{2}+0 $$

$$ T_{e}=\frac{3\times1005\times303+600\times10^{3}-3\times\frac{500^{2}}{2}}{3\times1005}=377.627\,\text{K}\ . $$

--- Ad ---

---

The density at the exit can be calculated using the ideal gas equation,

$$ \rho_{e}=\frac{p_{e}}{R\,T_{e}}=\frac{140\times10^{3}}{287\times377.6}=1.29176\,\text{kg/m}^{3} $$

Applying the conservation of mass equation,

$$ A_{e}=\frac{\dot{m}}{\rho_{e}V_{e}}=\frac{3}{1.29176\times 500} $$

$$ \boxed{A_{e}=0.0046448\,\text{m}^{2}}\ . $$

Applying the conservation of horizontal momentum,

$$ \text{Thrust}=\dot{m}_{e}V_{e}+\left(p_{e}-p_{\text{amb}}\right)A_{e} $$

$$ \text{Thrust}=3\times500+\left(140\times10^{3}-100\times10^{3}\right)\times0.0046448 $$

$$ \boxed{\text{Thrust}=1685.79\,\text{N}}\ . $$

Problem 1.13:

Solution: