Problem 1.12:
In a hydrogen-powered rocket, hydrogen enters a nozzle at a very low velocity with a
temperature and pressure of 2000oC and 6.8 MPa, respectively.
The pressure on the exit plane of the nozzle is equal to the ambient pressure,
which is 10 kPa. If the required thrust is 10 MN, what hydrogen mass flow rate is required?
The flow through the nozzle can be assumed to be isentropic and the specific heat ratio
of the hydrogen can be assumed to be 1.4.
Solution:
Given: \( \gamma_{h}=1.4 \)
\( V_{1}\approx 0 \),
\( T_{1} = T_{0} = 2000^{\circ}\,\text{C} = 2273\,\text{K} \),
\( p_{1}=p_{0}=6.8\,\text{MPa} \),
\( p_{e} = p_{\text{amb}} = 10\,\text{kPa} \),
\( \text{Thrust} = 10\,\text{MN} \)
To calculate: hydrogen mass flow rate?
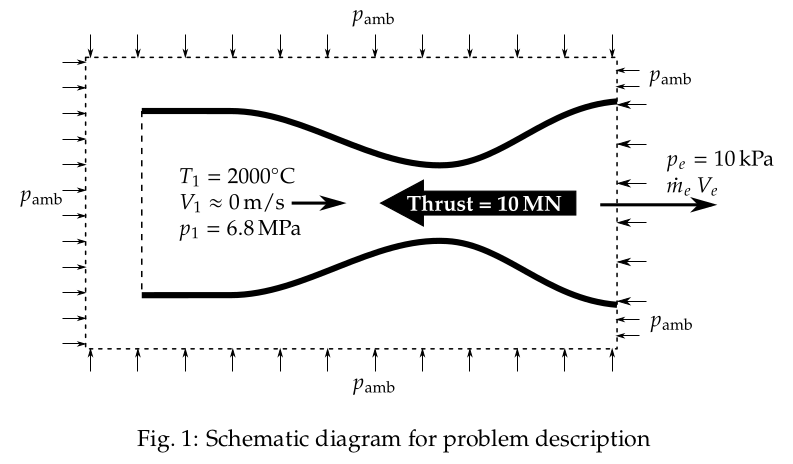
The schematic diagram of the problem description is shown in Fig. 1.
Using the molar mass of hydrogen as \( \hat{m}=2.016\,\text{kg/kmol} \) and universal gas constant as \( R_{u}=8314\,\text{J/kmol-K} \), the gas constant of hydrogen can be calculated as, $$ R=\frac{R_{u}}{\hat{m}} = \frac{8314}{2.016} = 4124\,\text{J/kg-K}\ . $$ The heat capacity of hydrogen at constant pressure can be calculated as, $$ c_{p}=\frac{\gamma_{h}R}{\gamma_{h}-1} $$ $$ c_{p} = \frac{1.4\times4124}{1.4-1} = 14434\,\text{J/kg-K}\ . $$
--- Ad ---
---
Since the flow through the nozzle can be assumed to be isentropic, $$ \frac{T_{e}}{T_{0}}=\left(\frac{p_{e}}{p_{0}}\right)^{\left(\gamma_{h}-1\right)/\gamma_{h}} $$ $$ T_{e}=T_{0}\left(\frac{p_{e}}{p_{0}}\right)^{\left(\gamma_{h}-1\right)/\gamma_{h}} $$ $$ T_{e}=2273\times\left(\frac{10\times10^{3}}{6.8\times10^{6}}\right)^{\left(1.4-1\right)/1.4}=352.623\,\text{K}\ . $$
Using the conservation of energy equation,
$$ c_{p}T_{0}=c_{p}T_{e}+\frac{V_{e}^{2}}{2} $$ $$ 14434\times2273=14434\times352.623+\frac{V_{e}^{2}}{2} $$which can be solved for exit velocity as,
$$ V_{e}=\sqrt{2\times\left(14434\times2273-14434\times352.623\right)}=7445.6325\,\text{m/s}\ . $$Using the conservation of momentum, since the exit plane pressure is same as ambient,
$$ \text{Thrust} = \dot{m}_{e}V_{e} $$Therefore, the mass flow rate is,
$$ \dot{m}_{e}=\frac{\text{Thrust}}{V_{e}}=\frac{10\times10^{6}}{7445.6325} $$ $$ \boxed{\dot{m}_{e}=1343.07\,\text{kg/s}}\ . $$