Given: \( \dot{m}_{e}=350\,\text{kg/s} \), \( V_{e}=750\,\text{m/s} \), \( p_{e}=75\,\text{kPa} \), \( D_{e}=⌀0.3\,\text{m} \).
To calculate:
(a) Thrust when \( p_{\text{amb}} = 100\,\text{kPa} \).
(b) Thrust when \( p_{\text{amb}} = 20\,\text{kPa} \).

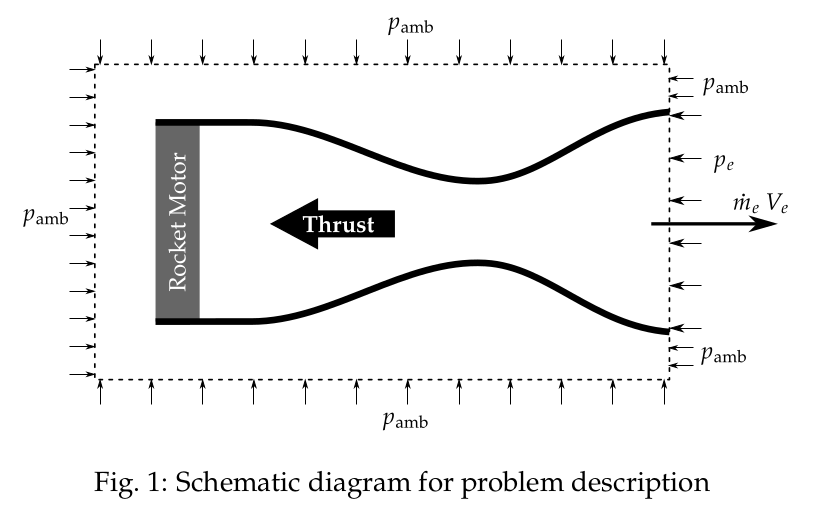
The schematic diagram of the problem description is shown in Fig. 1.

(a) Thrust when \( p_{\text{amb}} = 100\,\text{kPa} \).

Applying the conservation of momentum on the control-volume around the rocket,

$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{e}V_{e}-0+\left(p_{e}-p_{\text{amb}}\right)A_{\text{exit}}\\ \\ \text{Thrust} =&\ 350\times750-0+\left(75\times10^{3}-100\times10^{3}\right)\times\frac{\pi}{4}\times0.3^{2} \end{aligned} $$ $$ \text{when }\ p_{\text{amb}}=100\,\text{kPa}\quad\implies\quad\boxed{\text{Thrust}=260732.85\,\text{N}}\ . $$

(b) Thrust when \( p_{\text{amb}} = 20\,\text{kPa} \).

Applying the conservation of momentum on the control-volume around the rocket,

$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{e}V_{e}-0+\left(p_{e}-p_{\text{amb}}\right)A_{\text{exit}}\\ \\ \text{Thrust} =&\ 350\times750-0+\left(75\times10^{3}-20\times10^{3}\right)\times\frac{\pi}{4}\times0.3^{2} \end{aligned} $$ $$ \text{when }\ p_{\text{amb}} = 20\,\text{kPa}\quad\implies\quad\boxed{\text{Thrust}=266387.72\,\text{N}}\ . $$