Problem 1.10:
A rocket used to study the atmosphere has a fuel consumption rate of
kg/s
and a nozzle discharge velocity of
m/s.
The pressure on the nozzle discharge plane is
kPa.
Find the thrust developed when the rocket is launched at sea level. The nozzle exit plane diameter is
m.
Solution:
Given:
\( \dot{m}_{fuel}=120\,\text{kg/s} \),
\( V_{e}=2300\,\text{m/s} \),
\( p_{e}=90\,\text{kPa} \),
\( D_{e}=⌀0.3\,\text{m} \).
To calculate: Thrust at sea level.
The schematic diagram of the problem description is shown in Fig. 1.
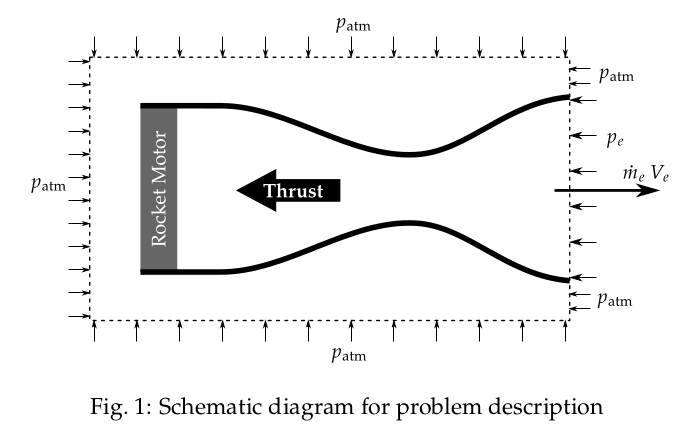
Assuming the atmospheric pressure at sea level as \( p_{\text{atm}}=1\,\text{atm}=101325\,\text{Pa} \).
Assuming that the oxidizer is mixed with the fuel, \( \dot{m}_{e}=\dot{m}_{fuel}=120\,\text{kg/s} \).
Applying the conservation of momentum on the control-volume around the rocket,
$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{e}V_{e}-0+\left(p_{e}-p_{\text{atm}}\right)A_{\text{exit}} \end{aligned} $$
$$
\text{Thrust} = 120\times2300-0+\left(90\times10^{3}-101325\right)\times\frac{\pi}{4}\times0.3^{2}
$$
$$
\boxed{\text{Thrust at sea level}=275199.483\,\text{N}}\ .
$$