Given: \( p_{1}=p_{2} \)
case 1 - without afterburner: \( \dot{m}_{1}=50\,\text{kg/s} \), \( \dot{m}_{1}:\dot{m}_{\text{fuel}}=90:1 \), \( V_{2}=600\,\text{m/s} \).
case 2 - with afterburner: \( \dot{m}_{1}=50\,\text{kg/s}, \) \( \dot{m}_{1}:\dot{m}_{\text{fuel}}=50:1, \) \( V_{2}=730\,\text{m/s} \).
To calculate: static thrust for case 1 and case 2.

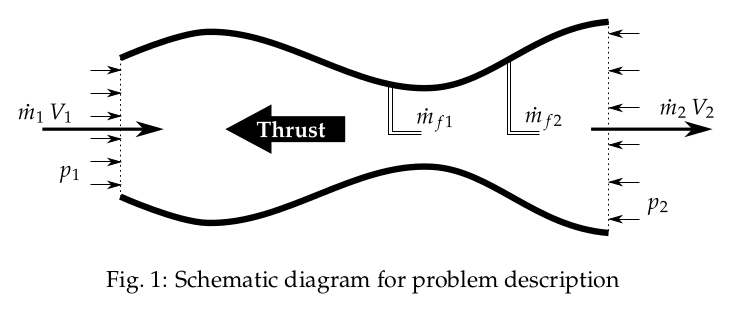
The schematic diagram of the problem description is shown in Fig. 1.

Case1: without afterburner

Using the conservation of mass,

Case1: without afterburner $$ \dot{m}_{2}=\dot{m}_{1}+\dot{m}_{f1}=\dot{m}_{1}+\dot{m}_{1}/90=50+50/90=50.556\,\text{kg/s}. $$

Assuming \( V_{1}\sim 0 \) (since engine is stationary on ground).

The conservation of momentum gives,

$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{2}V_{2}-\dot{m}_{1}V_{1}+\left(p_{2}-p_{1}\right)A_{\text{exit}}\\ \\ \text{Thrust} =&\ 50.555556\times600\\ \\ \text{Thrust} =&\ 30333.3336\,\text{N} \end{aligned} $$ $$ \boxed{\text{Static thrust}=30333.3336\,\text{N}}\ . $$

Case2: with afterburner

Using the conservation of mass,

$$ \dot{m}_{2}=\dot{m}_{1}+\left(\dot{m}_{f1}+\dot{m}_{f2}\right)=\dot{m}_{1}+\dot{m}_{1}/50=50+50/50=51\,\text{kg/s}. $$

Assuming \( V_{1}\sim 0 \) (since engine is stationary on ground).

The conservation of momentum gives,

$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{2}V_{2}-\dot{m}_{1}V_{1}+\left(p_{2}-p_{1}\right)A_{\text{exit}}\\ \\ \text{Thrust} =&\ 51\times730\\ \\ \text{Thrust} =&\ 37230\,\text{N} \end{aligned} $$ $$ \boxed{\text{Static thrust}=37230\,\text{N}}\ . $$