Problem 1.8

The engine of a small jet aircraft develops a thrust of 18 kN when the aircraft is flying at a speed of 900 km/h at an altitude where the ambient pressure is 50 kPa. The air flow rate through the engine is 75 kg/s and the engine uses fuel at a rate of 3 kg/s. The pressure on the engine discharge plane is 55 kPa and the area of the engine exit is 0.2 m². Find the jet efflux velocity.

Given:
Thrust = $ 18\,\text{kN} $, fuel rate = $ 3\,\text{kg/s} $
Inlet $ \rightarrow V_{1}=900\,\text{km/h}=900/3.6=250\,\text{m/s} $, $ p_{1}=50\,\text{kPa} $, $ \dot{m}_{1}=75\,\text{kg/s} $.
Outlet $ \rightarrow p_{2}=55\,\text{kPa} $, $ A_{\text{exit}}=0.2\,\text{m}^{2} $, $ V_{2}=?\,\text{m/s} $.

The schematic diagram of the problem description is shown in Fig. 1.

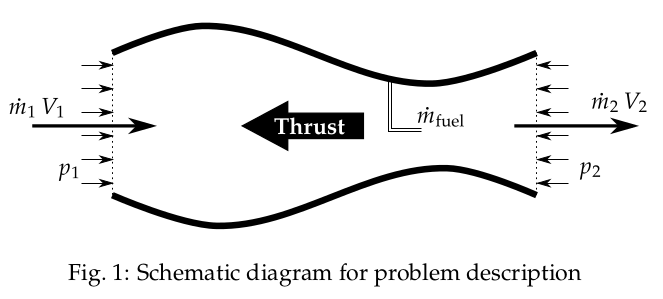
Using the mass conservation equation,

$$ \dot{m}_{2}=\dot{m}_{1}+\dot{m}_{\text{fuel}} $$ $$ \dot{m}_{2}=75+3=78\,\text{kg/s} $$

Using the conservation of momentum along horizontal direction,

$$ \begin{aligned} \text{Thrust} =&\ \text{rate of momentum exiting }-\text{ rate of momentum entering}\\ & +\text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}_{2}V_{2}-\dot{m}_{1}V_{1}+\left(p_{2}-p_{1}\right)A_{\text{exit}}\\ \\ 18\times10^{3} =&\ 78\times V_{2}-75\times250+\left(55\times10^{3}-50\times10^{3}\right)\times0.2 \end{aligned} $$ $$ V_{2}=\frac{18\times10^{3}+75\times250-\left(55\times10^{3}-50\times10^{3}\right)\times0.2}{78} $$ $$ \boxed{V_{2}=458.333\,\text{m/s}}\ . $$

Problem 1.8:

Solution: