Problem 1.7:
The jet engine fitted to a small aircraft uses 35 kg/s of air when the aircraft is
flying at a speed of 800 km/h. The jet efflux velocity is 590 m/s. If the pressure on
the engine discharge plane is assumed to be equal to the ambient pressure and if effects
of the mass of the fuel used are ignored, find the thrust developed by the engine.
Solution:
Given:
Inlet \( \rightarrow \) \( V_{1}=800\,\text{km/h}=800/3.6=222.22\,\text{m/s} \),
\( \dot{m}_{1}=35\,\text{kg/s} \)
Outlet \( \rightarrow \) \( V_{2}=590\,\text{m/s} \),
\( \dot{m}_{2}=35\,\text{kg/s} \) (ignoring fuel),
\( p_{2}=p_{1}=p_{\text{ambient}} \)
The schematic diagram of the problem description is shown in Fig. 1.
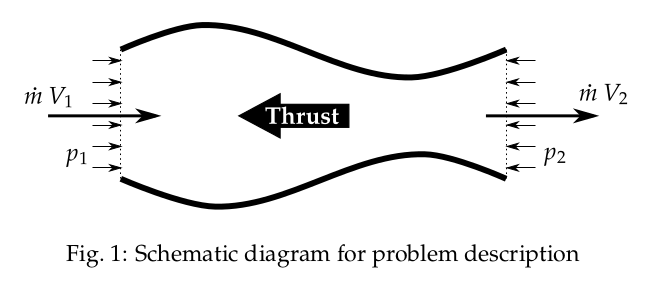
Using the conservation of momentum along horizontal direction,
$$ \begin{aligned} \text{Thrust} =&\ \text{ rate of momentum exiting }-\text{ rate of momentum entering}\\ &\ + \text{ pressure force at exit }-\text{ pressure force at inlet}\\ \\ \text{Thrust} =&\ \dot{m}V_{2}-\dot{m}V_{1}+\left(p_{2}-p_{1}\right)A_{\text{exit}}\\ \\ \text{Thrust} =&\ \dot{m}V_{2}-\dot{m}V_{1}+0\\ \\ \text{Thrust} =&\ \dot{m}\left(V_{2}-V_{1}\right)\\ \\ \text{Thrust} =&\ 35\times\left(590-222.22\right) \end{aligned} $$ $$ \boxed{\text{Thrust}=12872.3\,\text{N}} $$