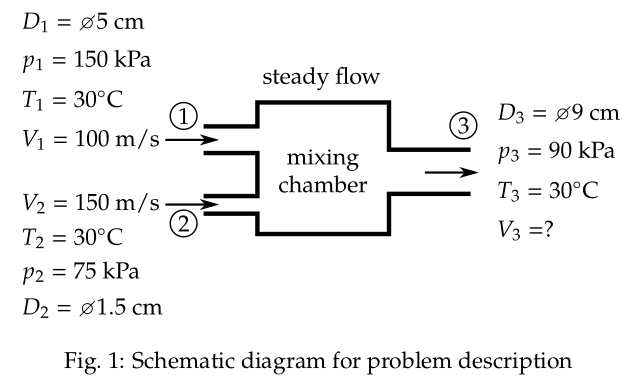
Problem 1.6

Two air streams are mixed in a chamber. One stream enters the chamber through a 5 cm diameter pipe at a velocity of 100 m/s with a pressure of 150 kPa and a temperature of 30^oC. The other stream enters the chamber through a 1.5 cm diameter pipe at a velocity of 150 m/s with a pressure of 75 kPa and a temperature of 30^oC. The air leaves the chamber through a 9 cm diameter pipe at a pressure of 90 kPa and a temperature of 30^oC. Assuming that the flow is steady, find the velocity in the exit pipe.

Given: Steady flow
- $T_{1} = 30^{\circ} C = 303 K$ , $p_{1} = 150 kPa$ , $D_{1} = ⌀ 5 cm$ , $V_{1} = 100 m/s$ (Inlet)
- $T_{2} = 30^{\circ} C = 303 K$ , $p_{2} = 75 kPa$ , $D_{2} = ⌀ 1.5 cm$ , $V_{2} = 150 m/s$ (Inlet)
- $T_{3} = 30^{\circ} C = 303 K$ , $p_{3} = 90 kPa, D_{3} = ⌀ 9 cm$ , $V_{3} = ? m/s$ (Outlet)

The schematic diagram of the problem description is shown in Fig. 1.

The densities of air at the various stations may be calculated using the respective pressures, temperatures and using the ideal gas equation.

ρ_{1} = \frac{p_{1}}{R T_{1}} = \frac{150 \times 10^{3}}{287 \times 303} = 1.7249 {kg/m}^{3}

ρ_{2} = \frac{p_{2}}{R T_{2}} = \frac{75 \times 10^{3}}{287 \times 303} = 0.86246 {kg/m}^{3}

ρ_{3} = \frac{p_{1}}{R T_{1}} = \frac{90 \times 10^{3}}{287 \times 303} = 1.0349 {kg/m}^{3}

--- Ad ---

---

Using the conservation of mass equation,

\begin{aligned} m_{1} + m_{2} & = m_{3} \\ ρ_{1} A_{1} V_{1} + ρ_{2} A_{2} V_{2} & = ρ_{3} A_{3} V_{3} \\ ρ_{1} \times \frac{π}{4} D_{1}^{2} \times V_{1} + ρ_{2} \times \frac{π}{4} D_{2}^{2} \times V_{2} & = ρ_{3} \times \frac{π}{4} D_{3}^{2} \times V_{3} \\ 1.7249 \times \frac{π}{4} \times {0.05}^{2} \times 100 + 0.86246 \times \frac{π}{4} \times {0.015}^{2} \times 150 & = 1.0349 \times \frac{π}{4} \times {0.09}^{2} \times V_{3} \end{aligned}

V_{3} = \frac{1.7249 \times \frac{π}{4} \times {0.05}^{2} \times 100 + 0.86246 \times \frac{π}{4} \times {0.015}^{2} \times 150}{1.0349 \times \frac{π}{4} \times {0.09}^{2}}

V_{3} = 54.915 m/s .

Problem 1.6:

Solution: