Problem 1.5

Two jets of air, each having the same mass flow rate, are thoroughly mixed and then discharged into a large chamber. One jet has a temperature of 120^oC and a velocity of 100 m/s, whereas the other has a temperature of -50^oC and a velocity of 300 m/s. Assuming that the process is steady and adiabatic, find the temperature of the air in the large chamber.

A schematic diagram of the configuration is shown in Fig. 1.
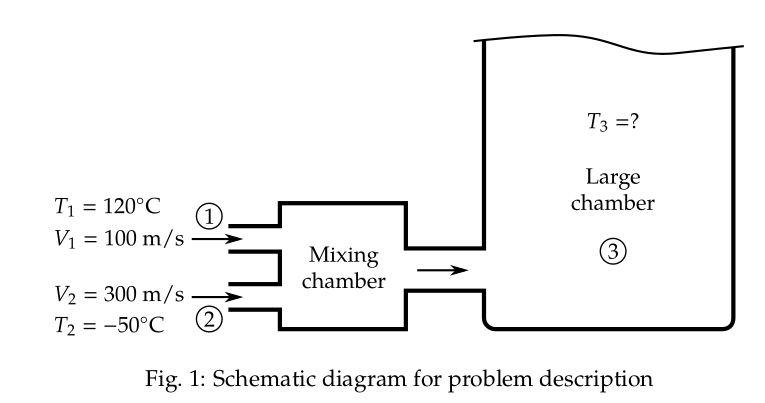
Schematic diagram of problem

Given: $T_{1}=120^{\circ}\text{C}=393\,\text{K}$ , $V_{1}=100\,\text{m/s}$ , $T_{2}=-50^{\circ}\text{C}=223\,\text{K}$ , $V_{2}=300\,\text{m/s}$ .

The mass flow rate is same through the two inlets, therefore,

$\dot{m}_{1}=\dot{m}_{2}=\dot{m}$

$\dot{m}_{3}=\dot{m}_{1}+\dot{m}_{2}=2\,\dot{m}$

--- Ad ---

---

Applying the conservation of energy equation (without heat and work),

$\left(\dot{m}_{1}\,c_{p}\,T_{1}+\dot{m}_{1}\frac{V_{1}^{2}}{2}\right) + \left(\dot{m}_{2}\,c_{p}\,T_{2}+\dot{m}_{2}\frac{V_{2}^{2}}{2}\right) = \left(\dot{m}_{3}\,c_{p}\,T_{3}+\dot{m}_{3}\frac{V_{3}^{2}}{2}\right)$

$\left(\dot{m}\,c_{p}\,T_{1}+\dot{m}\frac{V_{1}^{2}}{2}\right) + \left(\dot{m}\,c_{p}\,T_{2}+\dot{m}\frac{V_{2}^{2}}{2}\right) = \left(2\,\dot{m}\,c_{p}\,T_{3}+2\,\dot{m}\frac{V_{3}^{2}}{2}\right)$

$\left(c_{p}\,T_{1}+\frac{V_{1}^{2}}{2}\right) + \left(c_{p}\,T_{2}+\frac{V_{2}^{2}}{2}\right) = \left(2\,c_{p}\,T_{3}+2\frac{V_{3}^{2}}{2}\right)$

$T_{3}=\frac{c_{p}\,T_{1}+\frac{V_{1}^{2}}{2} + c_{p}\,T_{2}+\frac{V_{2}^{2}}{2} - V_{3}^{2}}{2\,c_{p}}$

Assuming $c_{p}=1005\,\text{J/kg-K}$ for air and the velocity in the large chamber to be effectively zero,

$T_{3}=\frac{1005\times393+\frac{100^{2}}{2}+1005\times223+\frac{300^{2}}{2}-0}{2\times1005}$

$\boxed{T_{3}=332.876\,\text{K}=59.8756^{\circ}\text{C}}$

Problem 1.5:

Solution: