Problem 1.1:
An air stream enters a variable area channel at a velocity of 30 m/s with a pressure of 120 kPa and a
temperature of 10oC. At a certain point in the channel, the velocity is found to be 250 m/s.
Using
Bernoulli's equation (i.e. \( p + \rho V^2/2 = constant \)), which assumes incompressible flow, find
the pressure at this point. In this calculation, use the density evaluated at the inlet conditions. If the
temperature of the air is assumed to remain constant, evaluate the air density at the point in the flow
where the velocity is 250 m/s. Compare this density with the density at the inlet to the channel. Based on
this comparison, do you think that the use of Bernoulli's equation is justified?
Solution:
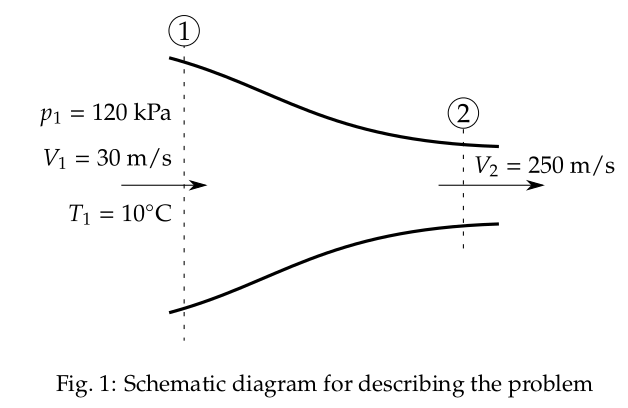
The problem description is schematically shown in Fig. 1.
Since the flow is assumed to be incompressible, \( \rho \) is constant and can be calculated at station 1 using ideal gas equation, $$ \rho=\rho_{1}=\frac{p_{1}}{R\,T_{1}}=\frac{120\times10^{3}}{287\times\left(10+273\right)}=1.47745\,\text{kg/m}^{3} $$ Using the Bernoulli's equation $$ p_{1}+\rho\,\frac{V_{1}^{2}}{2}=p_{2}+\rho\,\frac{V_{2}^{2}}{2} $$ which can be used to solve for pressure at station 2 $$ p_{2}=p_{1}+\frac{\rho}{2}\left(V_{1}^{2}-V_{2}^{2}\right) \qquad\leftarrow (eq.1) $$
Substituting \( \rho=1.47745\,\text{kg/m}^{3} \) in (eq.1), the pressure at station 2 can be calculated as, $$ p_{2}=p_{1}+\frac{\rho}{2}\left(V_{1}^{2}-V_{2}^{2}\right) $$ $$ p_{2}=120\times10^{3}+\frac{1.47745}{2}\left(30^{2}-250^{2}\right) = 74494.54\,\text{Pa} $$ $$ \boxed{\left.p_{2}\right|_{\text{incomp.}}=74.49454\,\text{kPa}} $$ If the temperature of the air is assumed to remain constant, \( T_{2}=T_{1}=283\,\text{K} \), then we can calculate the density at station 2 to be, $$ \rho=\frac{p_{2}}{R\,T_{2}}=\frac{74494.54}{287\times283} $$ $$ \boxed{\left.\rho\right|_{T=\text{constant}}=0.917183\,\text{kg/m}^{3}} $$ The percentage difference in calculated density, at station 1 and assuming constant temperature is, $$ \%\ \text{difference in density calculation} = \frac{\rho_{1}-\left.\rho\right|_{T=\text{constant}}}{\left.\rho\right|_{\text{Bernoulli}}}\times100 $$ $$ = \frac{1.47745-0.917183}{1.47745}\times100 = 37.92\% $$ Based on this comparison, it is clear that the use of Bernoulli's equation is not justified, as in an incompressible flow (with no heat transfer) the temperature variations are negligible. Therefore, the density calculated with this assumption must closely match with the result of Bernoulli's equation if the flow is indeed incompressible.

Since the flow is assumed to be incompressible, \( \rho \) is constant and can be calculated at station 1 using ideal gas equation, $$ \rho=\rho_{1}=\frac{p_{1}}{R\,T_{1}}=\frac{120\times10^{3}}{287\times\left(10+273\right)}=1.47745\,\text{kg/m}^{3} $$ Using the Bernoulli's equation $$ p_{1}+\rho\,\frac{V_{1}^{2}}{2}=p_{2}+\rho\,\frac{V_{2}^{2}}{2} $$ which can be used to solve for pressure at station 2 $$ p_{2}=p_{1}+\frac{\rho}{2}\left(V_{1}^{2}-V_{2}^{2}\right) \qquad\leftarrow (eq.1) $$
--- Ad ---
---
Substituting \( \rho=1.47745\,\text{kg/m}^{3} \) in (eq.1), the pressure at station 2 can be calculated as, $$ p_{2}=p_{1}+\frac{\rho}{2}\left(V_{1}^{2}-V_{2}^{2}\right) $$ $$ p_{2}=120\times10^{3}+\frac{1.47745}{2}\left(30^{2}-250^{2}\right) = 74494.54\,\text{Pa} $$ $$ \boxed{\left.p_{2}\right|_{\text{incomp.}}=74.49454\,\text{kPa}} $$ If the temperature of the air is assumed to remain constant, \( T_{2}=T_{1}=283\,\text{K} \), then we can calculate the density at station 2 to be, $$ \rho=\frac{p_{2}}{R\,T_{2}}=\frac{74494.54}{287\times283} $$ $$ \boxed{\left.\rho\right|_{T=\text{constant}}=0.917183\,\text{kg/m}^{3}} $$ The percentage difference in calculated density, at station 1 and assuming constant temperature is, $$ \%\ \text{difference in density calculation} = \frac{\rho_{1}-\left.\rho\right|_{T=\text{constant}}}{\left.\rho\right|_{\text{Bernoulli}}}\times100 $$ $$ = \frac{1.47745-0.917183}{1.47745}\times100 = 37.92\% $$ Based on this comparison, it is clear that the use of Bernoulli's equation is not justified, as in an incompressible flow (with no heat transfer) the temperature variations are negligible. Therefore, the density calculated with this assumption must closely match with the result of Bernoulli's equation if the flow is indeed incompressible.